The Square of Nine isn’t just about odd and even square numbers. It also involves the number eight (8) in its calculations. Each time the Square of Nine goes around, it adds eight more numbers to the previous round. It’s like stepping up a ladder, one rung at a time.
For example, in the first go, we have eight numbers from 2 to 9. In the second round, we add another eight to make 16 numbers from 10 to 25. And it continues like that. Here’s a breakdown of the first nine rounds:
- Round 1: 8 numbers from 2 to 9
- Round 2: 16 numbers (8×2=16) from 10 to 25
- Round 3: 24 numbers (8×3=24) from 26 to 49
- Round 4: 32 numbers (8×4=32) from 50 to 81
- Round 5: 40 numbers (8×5=40) from 82 to 121
- Round 6: 48 numbers (8×6=48) from 122 to 169
- Round 7: 56 numbers (8×7=56) from 170 to 225
- Round 8: 64 numbers (8×8=64) from 226 to 289
- Round 9: 72 numbers (8×9=72) from 290 to 361
Now, let’s talk about how to figure out how many cells are in each round of the Square of Nine:
- Start with the odd square number that finishes the round (for example, 361).
- Find the square root of that number (in this case, it’s 19).
- Divide the result from step 2 by 2 (so, 19/2 = 9.5).
- Subtract 0.5 from the answer in step 3 (which gives us 9).
- Multiply the answer from step 4 by 8 (resulting in 72).
This means there are 72 cells in the round that ends with the number 361. This method works for any round in the Square of Nine.
There is another way which we already discussed earlier. It is with the concept of “Size”.
A Gann Square of 9 with Size 6 will be a grid of 6th odd number.
It means it will be a grid of 11 as you can see it is 6th odd number from the odd number’s sequence of 1, 3, 5, 7, 9, 11… Etc.
11×11 grid has 121 numbers.
The above approach shows that Gann Square of 9 has many ways of effective calculations!
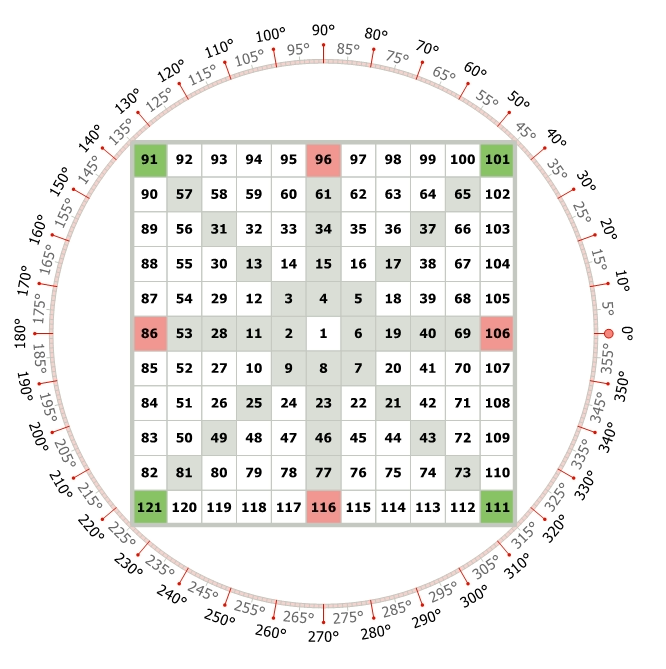
In another note, Let’s say You are given the number of 121 and is tasked to find the previous numbers that lie in the cardinal and ordinal crosses.
The numbers are marked here in above with green and red color. Now, although, we can calculate it using the property of “Square of Odds”, there is another way to do so!
Let’s revisit the concept of Sizes. The number 121 and the problems i.e. the numbers we need to find are on the Round 5 in this Size 6 Gann Square of Nine.
Now, if We recall from back,
In Round 5, there are 40 numbers (8×5=40) from 82 to 121.
So, Let’s make eight equal parts of eight equal directions! 40/8 = 5. Hence the numbers are –
- 121 – 5 = 116
- 116 – 5 = 111
- 111 – 5 = 106
- 106 – 5 = 101
- 101 – 5 = 96
- 96 – 5 = 91
- 91 – 5 = 86
The reason the number “8” matters is that it also signifies 8 sides and allows the numbers to get divided by 8! It breaks the Gann Square of 9 into eight equal parts.
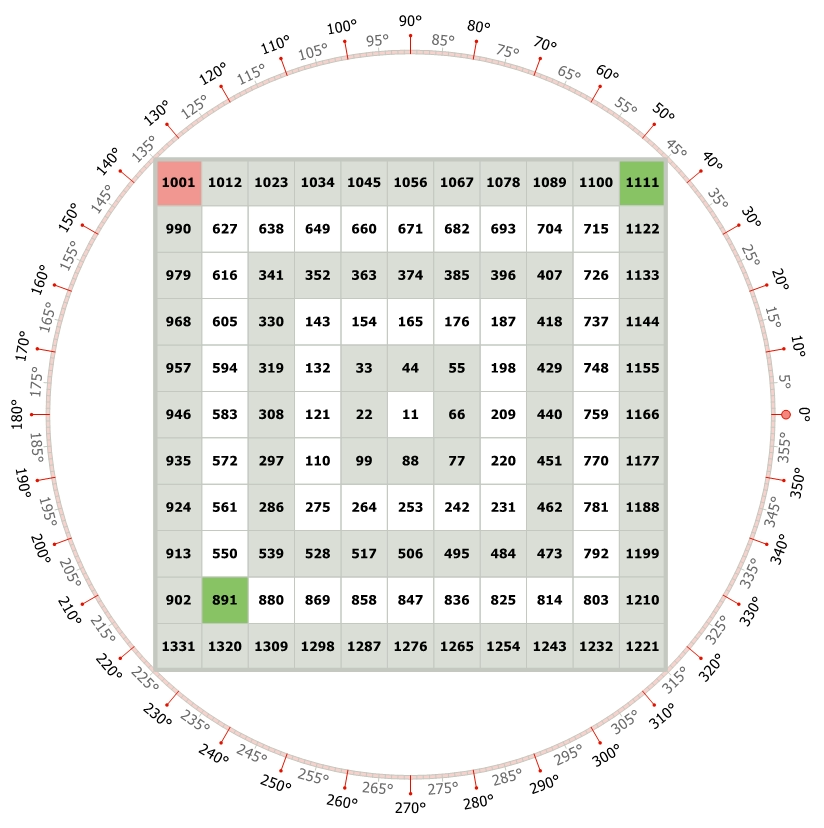
We can indulge the same properties of equidistance into more complex calculations. Like in the image above, The Gann Square of 9 is an unconventional one.
The apex value is 11. It has an increment of 11. Let’s say we know the values that are marked in green in the above image i.e., 891 and 1111. Can We find the number marked in the red color?
- 891 is the starting cell that spiral outwards.
- In other words, the distance between 891 and 1111 divides the outer base where 1111 lies into 2 equal parts.
- To get the red cell’s value we need to divide it by 4 equal parts.
So, Answer is 891 + ((1111-891)/4) *2 = 891 + (55*2) = 891 + 110 = 1001.
The mathematical complexity increases in each step as We step into deeper into the understanding.