In his discussions about the 360° movement of numbers on the Square of Nine, W.D. Gann utilized the terms “square” and “cycle.” We will analyze Square of Nine from William Gann’s perspective.
Here is what it’s about:
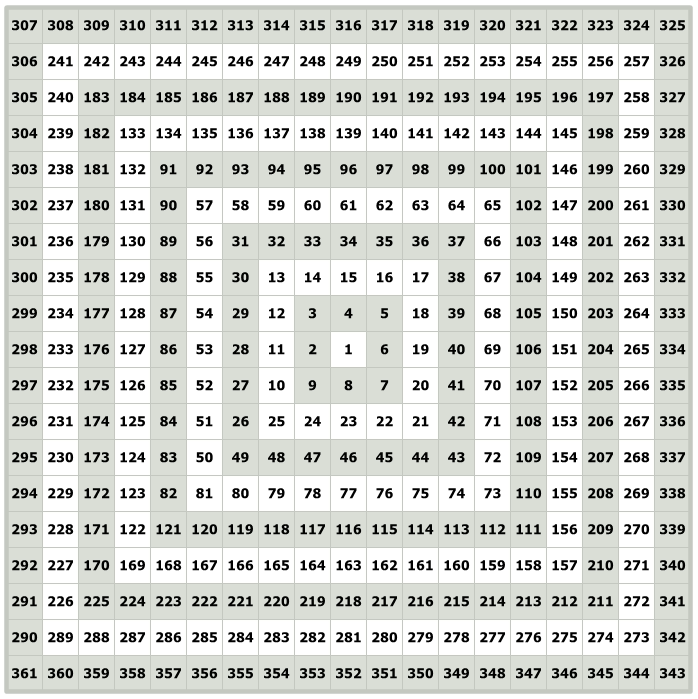
- The basic form is a square.
- The principle of making this square is very ingenious.
- The numbers are arranged in increasing order, in a specific pattern, starting with the number one set in the center.
- We can arrange as many numbers as we wish.
- The numbers can be arranged starting from the middle, to the right and up, in a counterclockwise manner, or to the left and up, in a clockwise manner.
When setting the Square of Nine we have to consider the trend’s direction.
If the trend is ascending, we will arrange the numbers clockwise, if it is descending, we will arrange the numbers counterclockwise.
However, this is a norm or standard practice. Nothing is enforceable and the end results do not variate based on this decision.
Construct A Basic Gann Square of 9
- Start with a square grid.
- Place the number 1 in the center (apex) of the grid.
First Cycle:
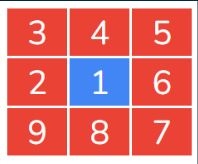
- Place the number 2 immediately to the left of 1. This starts the First Cycle.
- Continue placing numbers in a clockwise spiral pattern around the center, moving outward.
- The first complete cycle around the center adds 8 more numbers to the grid.
- The first cycle completes with the number 9.

The Next Cycles:
- The 2nd cycle starts at 10 and goes up to 25.
- The 3rd cycle starts at 26 and goes up to 49.
- The 4th cycle starts at 50 and goes up to 81.
And, So on…
The Word “Square”
In this context, the term “squaring” doesn’t involve calculating the mathematical square of a number.
Rather, it refers to the spiral-like mathematical arrangement of numbers within a Square Grid.
“Size” of Gann Square of 9
Now comes the concept of Size –
In the above, The Gann Square of 9 is said to have a size of 5. It is because it has 5 levels of spirals.
The fact that It is a 9×9 grid does not mean anything with Gann Square of 9. It is a 9×9 grid having 81 numbers because a Gann Square of 9 with size 5 will have a grid of 5th odd numbers. 5th odd number is 9.
Similarly,
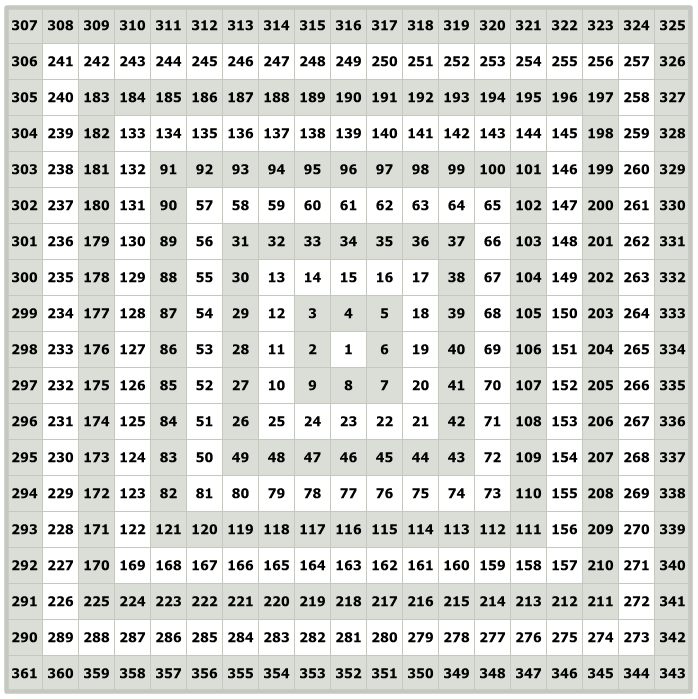
A Gann Square of 9 with size 10 will have a grid of 10th odd numbers. The 10th odd number is 19. So, it is a grid of 19×19 with 361 total numbers in it.
Similarly, The above Gann Square of 9 has a size of 4.

This one has a size of 3.
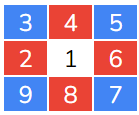
This one has a size of 2.
“Increment” in Gann Square of 9
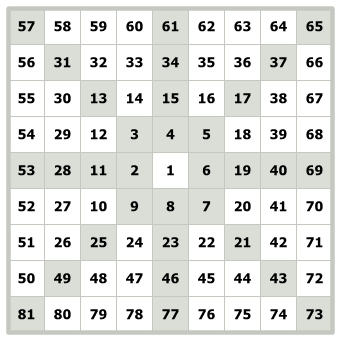
Now comes the concept of Increment –
In the above, The Gann Square of 9 is said to have an increment of 1. It is because it is increasing by 1 in terms of value in each step.

Similarly, the above Gann Square of 9 has an increment of 10.

Similarly, the above Gann Square of 9 has an increment of .2.
Starting Point in Gann Square of 9
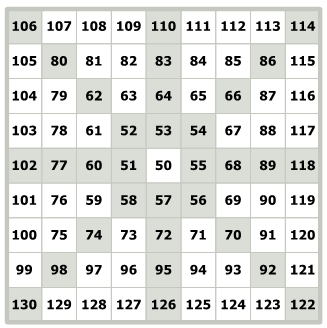
In the above, The Gann Square of 9 is said to have an increment of 1 and it started from the number 50.
- It can start from any number.
- It can have any increment.
With the reference of Pyramid’s Apex Point, The Starting Point is called said Apex Value
Now Notice –
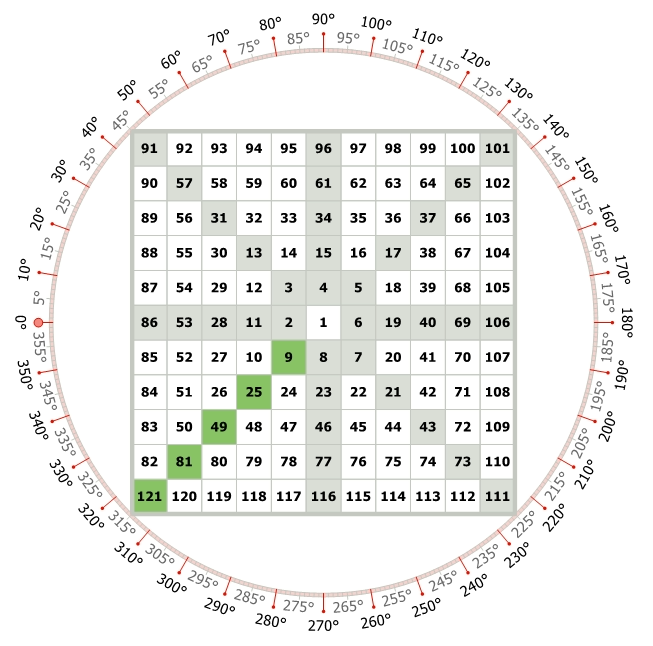
For instance, in the above Figure, the progression from 26 to 49 or 50 to 81 or 52 to 121, or 122 to 169 constitutes a single 360° movement, which Gann referred to as a square or cycle.
However, due to the potential confusion arising from the multiple meanings of these terms, this book opts to use the term “rotation” to denote a complete 360° movement on the Square of Nine.
Each rotation is represented by alternating backgrounds of white and gray. W.D. Gann characterized a rotation by the highest number within that rotation, which consistently concludes the sequence. For instance, the rotation spanning from 82 to 121 is designated as the rotation concluding with the number 121, or the rotation of 121.
W.D. Gann constructed his Square of Nine on graph paper, with each number allocated to a specific graph square. In this context, a graph square housing a single number is referred to as a “cell.”
In the Square of Nine depicted above,
- It started from 1 and got increased by 1 in the next steps.
- So, the number 147 occupies cell 147.
In the previous examples of the Square of Nine presented, the numbers located on the square’s surface follow a clockwise rotational pattern. A closer examination of W.D. Gann’s private work uncovers a handful of instances where he constructed Square of Nine charts with a counterclockwise rotation.
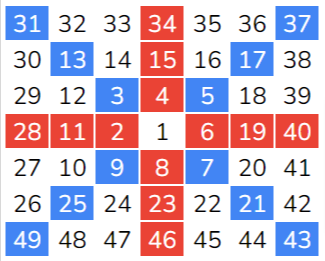
On this page, you’ll find four straightforward Square of Nine depictions.
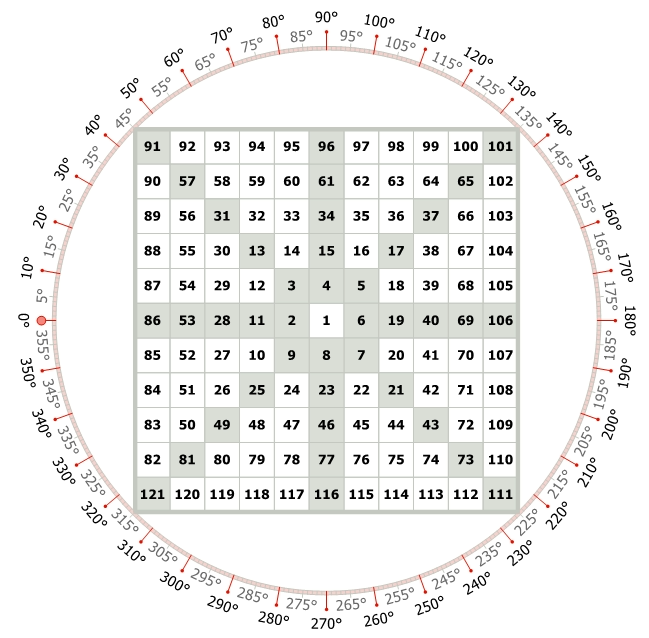
This figure of Gann Square of 9 illustrates – Numbers moving in a clockwise rotation and Angles moving in a clockwise rotation.
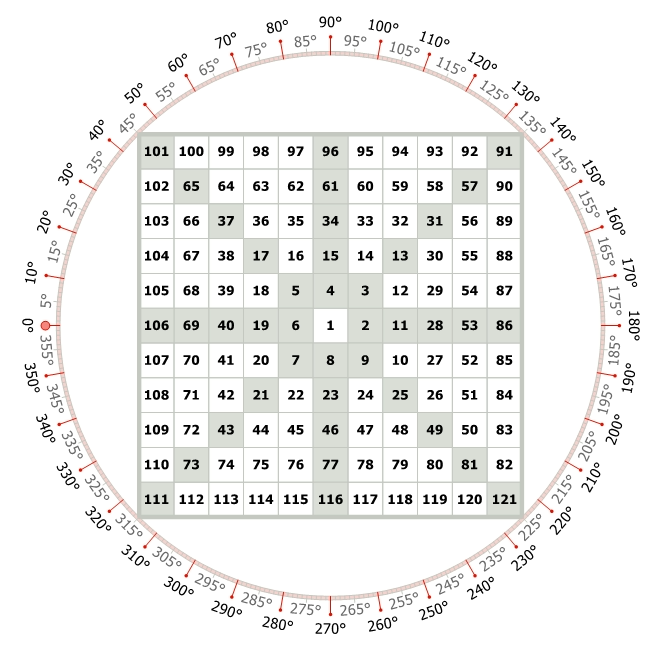
This figure of Gann Square of 9 illustrates – Numbers moving in an anticlockwise rotation and Angles moving in a clockwise rotation.
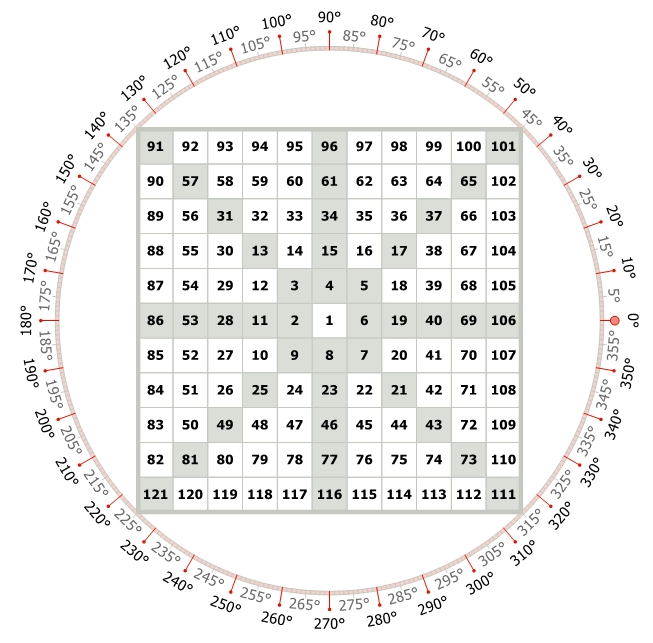
This figure of Gann Square of 9 illustrates – Numbers moving in a clockwise rotation and Angles moving in an anticlockwise rotation.
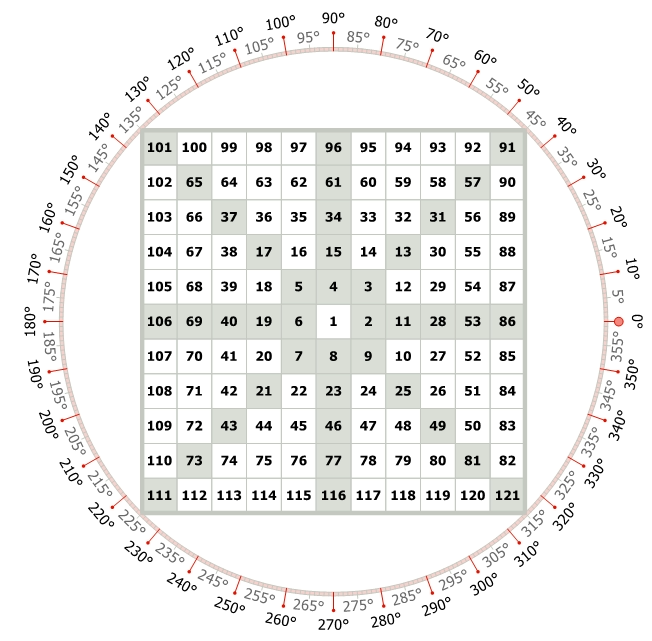
This figure of Gann Square of 9 illustrates – Numbers moving in an anticlockwise rotation and Angles moving in an anticlockwise rotation.
While W.D. Gann mostly designed Square of Nine charts to move in a clockwise manner, a thorough investigation into both clockwise and counterclockwise movements was carried out. Surprisingly, the findings showed that the outcomes are quite similar regardless of the direction.
To ensure simplicity and coherence, this book mostly sticks to the clockwise rotation, which is what W.D. Gann himself often preferred.