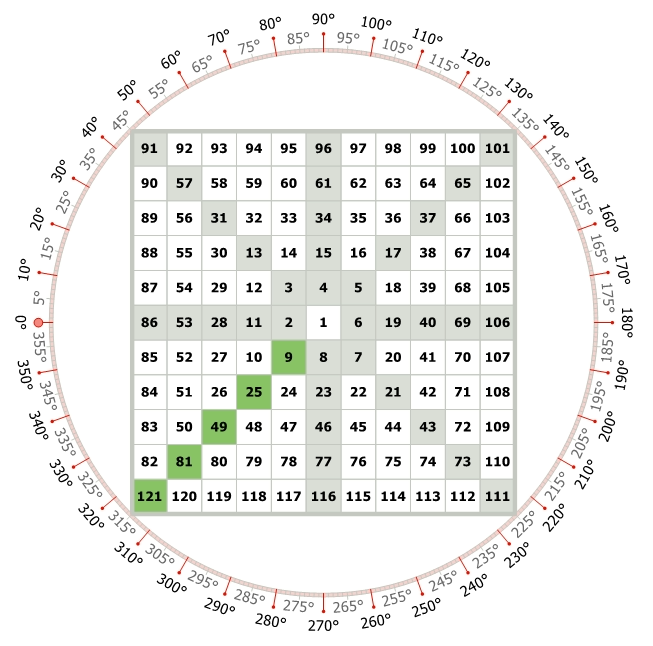
After arranging the numbers, we can observe some special similarities forming. For example, on one diagonal we have the numbers 1, 9, 25, 49, 81, 121, 169, and so on.
These numbers are marked in green color in the above image.
Notably, 9 is the square of 3 (3 multiplied by 3 equals 9).
The subsequent numbers in this sequence represent the square’s odd numbers which are 5, 7, 9, and 11.
It’s worth highlighting that the squares of odd numbers are consistently aligned with the lower left corners in each rotation. It means – These odd-number squares always occupy the final position within their respective rotations.
- 1^1 = 1
- 3^3 = 9
- 5^5 = 25
- 7^7 = 49
- 9^9 = 81
- 11^11 = 121
This is called the “Square of Odd” Property of Gann Square of Nine.