As we explore the Square of Nine and move from even square numbers to odd square numbers, or the other way around, we find some interesting points along the way.
- First, we come across First quarter points,
- Then halfway points,
- And finally third quarter points.
- Then we land into either “Square of Odd” or “Square of Even”.
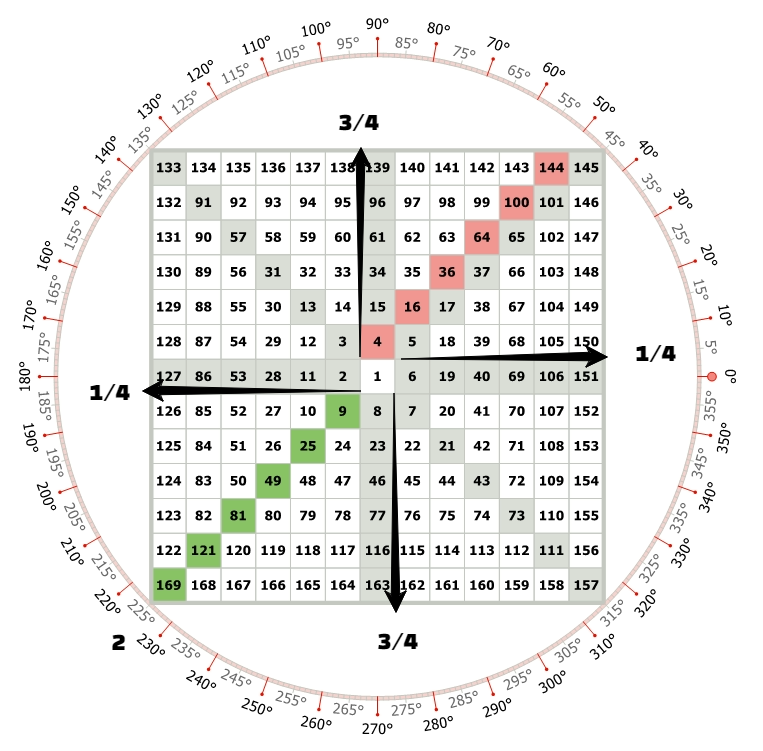
Then it repeats.
Think of these points like markers that help us understand what’s happening. These markers show up as we go through the numbers. They’re like signposts on a journey. We have already discussed about Halfway Points in our previous discussion.
Like, in the journey from 100 to 121,
- The halfway point between 100 to 121 is
100 + (121-100)/2
= 100 + (21/2)
= 100 + 10.5
= 110.5 - The First Quater Point is half of halfway point and starting point, i.e., 100 + (110.5 – 100)/2
= 100 + 5.25
= 105.25
Anyways, Now,
- The Third Quater Point is half of halfway point and ending point, i.e., 110.5 + (121 – 110.5)/2
= 110.5 + 5.25
= 115.75
If the Numbers that fall into Square of Odd and Square of Even are whole number,
- Then the halfway number will end with .5 and,
- The First quarter numbers will end with .25 and,
- The Third quarter numbers will end with .75.
Now, these points are not regular whole numbers like 1, 2, or 3. They’re in between the regular numbers on the Square of Nine.
To make it clearer:
Now, these points play a role in splitting a complete turn between consecutive odd square numbers. In this case, these points mark the steps of one-eighth as we go all the way around the full rotation.
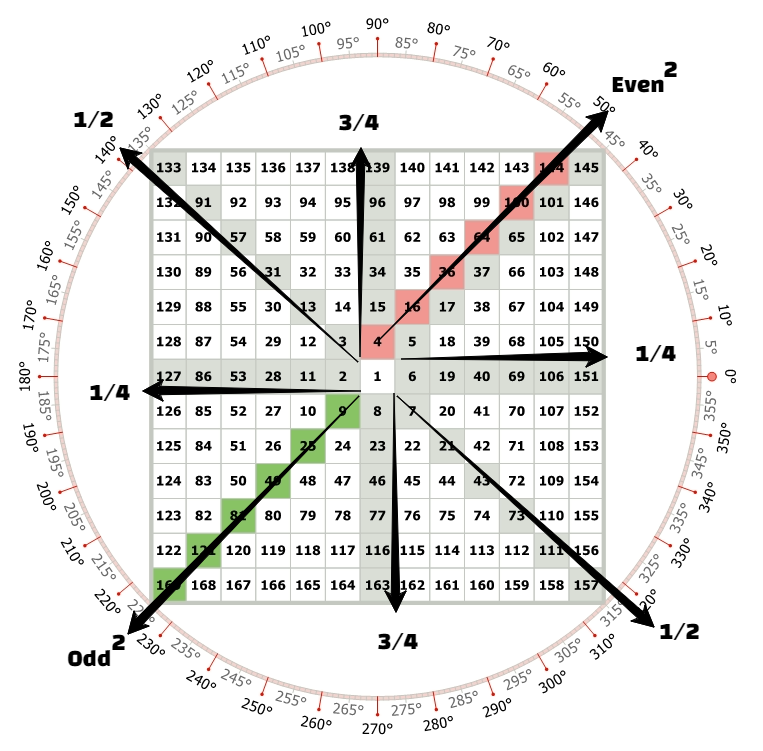
Quarter (1/4) Points:
They split the numbers between even and odd square numbers on the right or left sides.
Halfway (1/2) Points:
- They show up as you move from even to odd numbers, going down and to the right.
- When you go from odd to even numbers, they go up and to the left.
Three Quarter (3/4) Points:
- These appear at the bottom when you’re going from even to odd numbers,
- And at the top when you’re going from odd to even numbers.
They help divide a full rotation between odd square numbers, and each point represents a little part of that rotation.