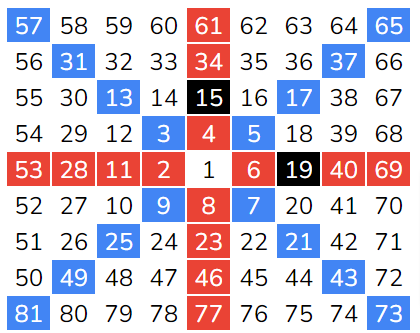
We are given a number; Our Goal is to Find Support and Resistance. So We need to construct the Gann Square of 9 and identify the closest Cardinal and Ordinal Cross numbers.
The problem happens when the number is of higher value –
- The Size of the Gann Square of 9 needs to be higher and,
- It is hard to construct and visualize higher Gann Grids.
Let’s take a Reference Point – Let’s say the LTP of a stock is 5152. Let’s generate a Gann Square of 9 based on this –
#1 Square of Odds
Let’s start by using the Square of Odds principle. Our goal is to locate the nearest odd number that is also a perfect square.
Step 1: Calculate the square root of 5152, which is approximately 71.77743378.
Step 2: Round down this value to the closest odd number, giving us 71.
Step 3: Find the square of 71, which equals 5041.
It’s important to note that while the technique involves rotating the Gann Wheel, it’s similar but not identical. Additionally, for the rotation process, rounding up was required.
#2 Finding Cardinal
Now, let’s apply the Gann Angle concept to discover the number that corresponds to a 45-degree rotation from 5041, which is our original value.
Taking into account the 360-degree rotation reference:
Did you observe our adjustment by subtracting the number “2”? In this context, if we consider “2” as representing a complete 360-degree i.e., one rotation, then:
- “1” would symbolize a 180-degree i.e., one-half rotation,
- “.5” would denote a 90-degree i.e., one-fourth rotation, and
- “.25” would equivalently represent a 45-degree i.e., one-eighth rotation.
Coming back to our calculation:
Starting with the original number 5041:
Step 1: Compute the square root of 5041, resulting in 71.
Step 2: Adding 0.25 to this value leads us to 71.25.
Step 3: Squaring the adjusted value of 71.25 yields 5077 (rounded up).
#2 Important Levels
Now that we grasp the Gann Angle concept and its connection to turning, let’s keep exploring pivot points. Remember, cardinal and ordinal numbers act like important markers, and they have a unique link: they’re separated by exactly 45 degrees. This interesting link pushes us ahead as we work out pivot points.
A pivot point is a significant price level in trading that can serve as a reference for assessing potential price movements. It’s a point where the market sentiment can shift, and traders often use pivot points to make decisions about entry, exit, and risk management.
Pivot points can act as both support and resistance levels.
- When the price of an asset is falling and reaches a pivot point, it might find support there.
- On the flip side, when the price of an asset is rising and reaches a pivot point, it might encounter resistance.
Starting from our original number 5041:
Pivot Point Calculation 1:
- Step 1: Find the square root of 5041, which gives us 71.
- Step 2: Add 0.25 to 71, making it 71.25.
- Step 3: When we square 71.25, we get 5112 (rounded up).
Pivot Point Calculation 2:
- Step 1: By adding 0.25 to 71.5, we reach 71.75.
- Step 2: When we square 71.75, we end up with 5148 (rounded up).
Pivot Point Calculation 3:
- Step 1: Continuing forward, we add 0.25 to 71.75, resulting in 72.
- Step 2: When we square 72, we get 5184 (rounded up).
This process shows us how to find pivot points step by step, moving 45 degrees from the starting value of 5041.
In short,
- 71.25+.25=71.5
- Square of 71.25 = 5112 (rounded up)
- 71.5+.25=71.75
- Square of 71.25 = 5148 (rounded up)
- 71.75+.25=72
- Square of 72 = 5184 (rounded up)
.25 here means one-eight rotation indeed.
Discussion – To move a starting number three-fourths of one rotation, calculate the number to add or subtract by multiplying 3/4 or 0.75 by 2. This yields 1.5.
The Solution
Thus, we’ve arrived at the range of 5148 < 5152 < 5184. Basically, as all the numbers from Cardinal and Ordinal are Pivot Points, we check between which two Pivot Points the current number lies to get our answer!
At 5148, we find a support level.
Conversely, at 5184, we encounter resistance.
By performing calculations involving nearby Cardinal and Ordinal Numbers, we’ve successfully constructed Gann’s Square of 9 Levels. It also eliminates the necessity to painstakingly sketch out the complete chart.
We got the solution without even visualizing it.
So far, you have learned – How to calculate the support and resistance using Gann Square of 9.